Haskell style Infinite Sequences in Python? It's easier than you think!

#python #itertools #iterators #infinitesequences

Let's say you need to continuously generate a bunch of information and send it as a signal to another system, or you need to perform a harmonic analysis for your project, or you have to perform an operation on an undefined number of inputs until a specific condition is met. These fall into the domain of "Infinite Sequences" and are not alien to the world of Data Science.

In fact, infinite sequences are natural to programming languages such as Haskell. Here is a great video from Computerphile to demonstrate that.

But did you know that you can work with infinite sequences quite efficiently in Python as well? You can write while loops but a pythonic way would be to create iterators that you can use. In fact, itertools has some very interesting out-of-the-box methods called "infinite iterators" for you to work with infinite sequences.

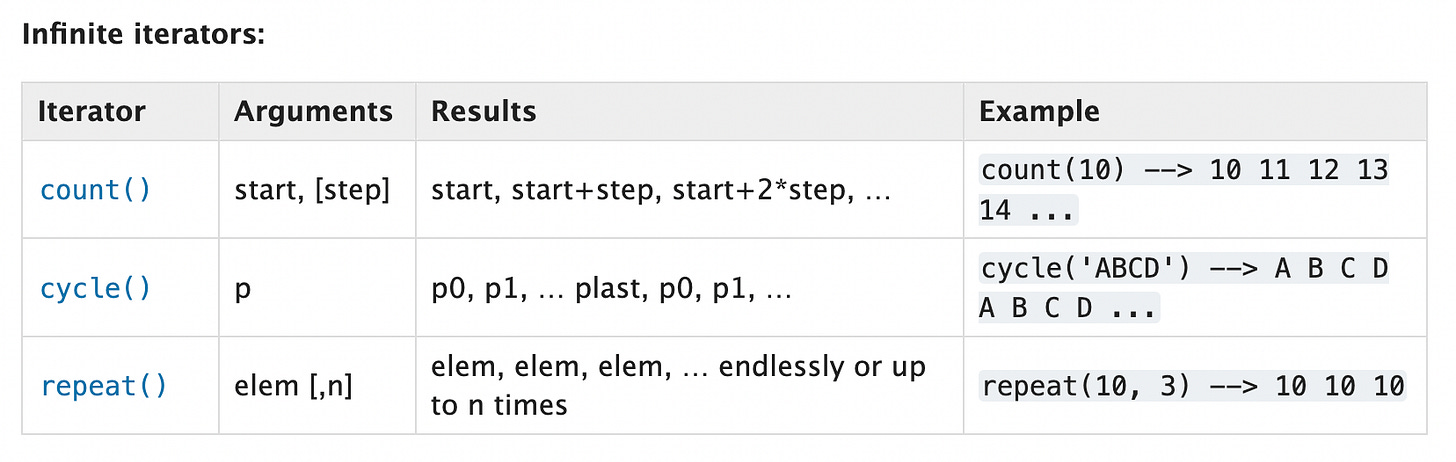
There are 3 infinite iterators in itertools that you can work with -

---

Working with Infinite Iterators

Let's start with a simple example of generating prime factors for an infinite sequence of multiples of 5 greater than 100 -

#!pip install sympy
from itertools import count, islice
from sympy.ntheory import primefactors

itr = count(start=100,step=5)      #<-- infinite sequence
f = lambda x: (x, primefactors(x)) #<-- fx for prime factors

factors = map(f, itr)              #<-- map the function

list(islice(factors, 10))          #<-- get first 10 elements

 (105, [3, 5, 7]),
 (110, [2, 5, 11]),
 (115, [5, 23]),
 (120, [2, 3, 5]),
 (125, [5]),
 (130, [2, 5, 13]),
 (135, [3, 5]),
 (140, [2, 5, 7]),
 (145, [5, 29])]

You can see the power of this. The map() + count() structure can get super complex super, fast with more advanced operations, and all of this, without defining a close set of inputs. Then during inference, you could use itertools.islice or just a simple for loop to infer them as per need with lazy execution.

Here is another example of summing 2 infinite sequences -

iter1 = count(10,2)         #<-- inf seq start 10, step 2
iter2 = count(5,3)          #<-- inf seq start 5, step 3
g = lambda x, y: (x,y,x+y)  #<-- sum function

inf_sum = map(g, iter1, iter2) #<-- map the function

list(islice(inf_sum, 10))   #<-- get first 10 elements

[(10, 5, 15),
 (12, 8, 20),
 (14, 11, 25),
 (16, 14, 30),
 (18, 17, 35),
 (20, 20, 40),
 (22, 23, 45),
 (24, 26, 50),
 (26, 29, 55),
 (28, 32, 60)]

You have a few more options to build infinite sequences using itertools.cycle and itertools.repeat -

from itertools import cycle

iter3 = itertools.cycle(['A','B','C'])
list(islice(iter3, 10))

## ['A', 'B', 'C', 'A', 'B', 'C', 'A', 'B', 'C', 'A']

from itertools import repeat

iter4 = itertools.repeat('hello world') #<-- pass any object
list(islice(iter4, 5))

## ['hello world', 'hello world', 'hello world', 'hello world', 'hello world']

And, you can mix and match these iterators with your functions using map().

I worked with these iterators for creating a batch-wise Numpy computation. My Numpy operation was taking a ton of memory due to a large number of input vectors and so I needed a strategy where I could break the large computation task into smaller batches. The function I wrote would take a batch of vectors, run a vectorized operation on them, save the output, and then fetch the next batch. This would work infinitely until it met a break condition.

This was a very high-level overview of the world of infinite sequences using Python. Hope this gives you some ideas when working on your next project involving such functions!